[Binary Search && Two pointer]BJ_3151, 합이 0

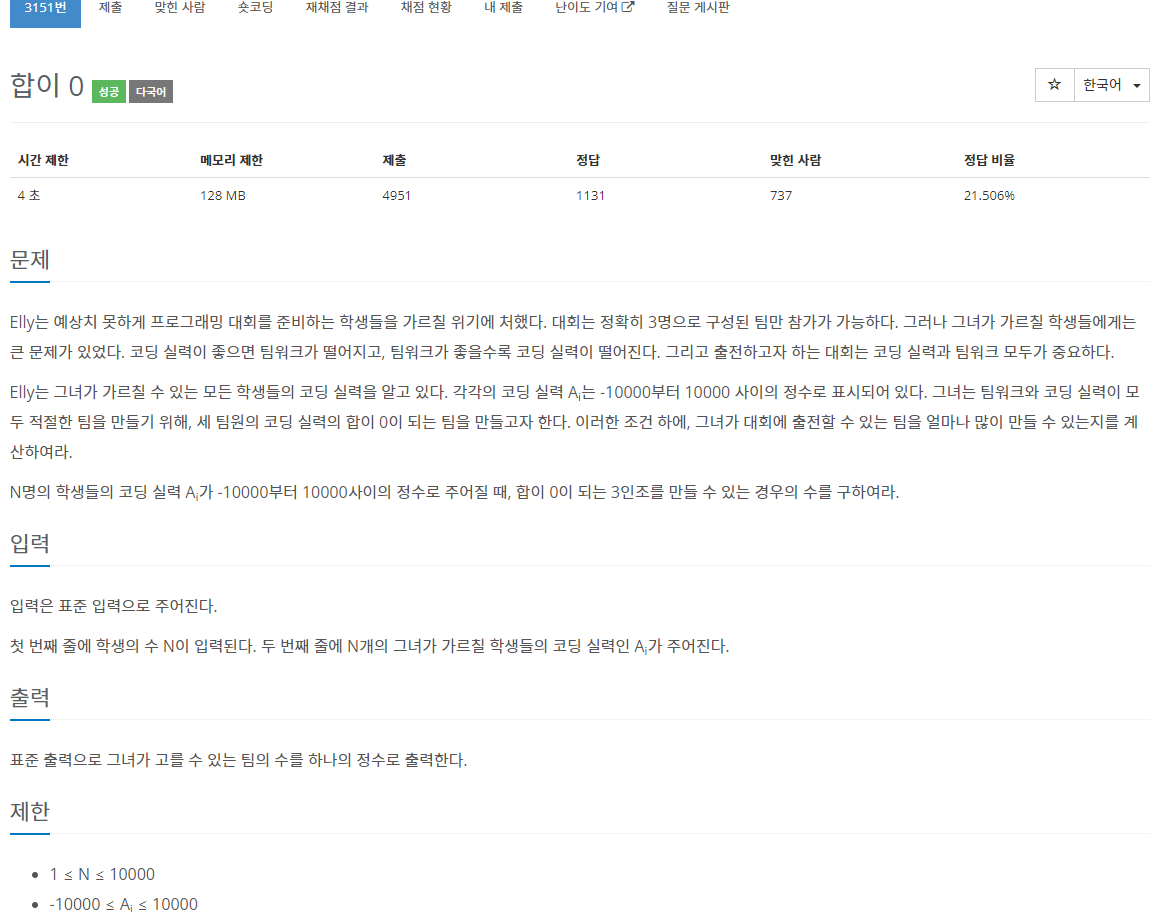
[문제의 접근]

 수학 논리적으로 생각해 보았을 때, 위의 문제는 문제의 복잡도가  $O(n^3)$ 인 문제로 N이 충분히 작다면 Bruteforce로 풀리는 문제라고 생각해 볼 수 있다. 그런데 N이 10000 으로 주어졌기 때문에 Bruteforce는 불가능하다. 그렇다면 $O(n^2 log(n)$ 이나 $O(n^2)$의 접근법을 생각해 보아야 한다. 전자의 경우는 시간 초과가 날 것 같은 우려가 있지만, 제한 시간이 4초 이기 때문에 가능성이 있어 보인다. 방법론은 Lower_bound 와 Upper bound를 이용해서 푸는 방법이다. 후자의 경우는 Two-pointer를 이용하면 될 것 같다. 세 수의 합이 0이 되는 조건을 찾는 문제인데, 합은 숫자의 크기에 의존하고 수의 크기는 정렬이 가능하므로 이분 탐색을 생각할 수 있어야 한다. 

 

[Lower_bound && Upper_bound]

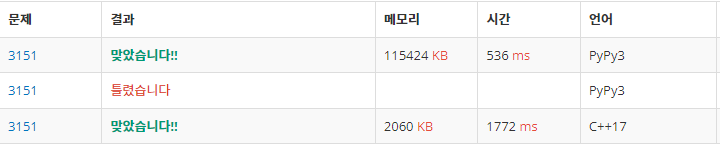
 시간 초과의 우려가 있는 문제는 Python보다는 C++이 유리하다. 아래와 같이 주어진 배열을 일단 sorting을 진행한다. 이 부분을 빼먹는 경우가 종종 있으니 꼭 기억하고 수행하자. 2중 for문을 구성해서 배열을 돌리면서 현재 주어진 두수의 합의 역수를 구하는데, 동일한 값이 주어질 수 있기 때문에 upper_bound에서 lower_bound를 뺀 값, 즉 동일한 값들을 모두 구해 주어야 한다. 한가지 주의해야 할 점은 주어진 배열이 모두 0일 경우는 경우의 수가 $_{10000}C_3$ 이 되어서 int의 범위를 벗어나기 때문에 정답을 저장하는 sol 변수는 long long으로 선언해야 한다는 점이다. 

 

sort(&arr[0], &arr[n]);
// 첫 두수를 정하고 lower bounds와 upper bounds를 구해서 그 차이 값으로 최종 카운트
// 배열 모두가 0이라면 10000C3가 되어, int 범위 초과 
// long long을 사용해야 한다. 
long long sol = 0;

for (int i=0; i<=n-3;i++) {
    for (int j=i+1; j<=n-2;j++) {
        int _sum = arr[i]+arr[j];
        if (_sum >0) continue; // 가지치기 500ms 줄임
        sol += upper_bound(j+1, -_sum) - lower_bound(j+1, -_sum);
    }
}

 

Lower_bound와 Upper_bound의 경우는 library를 사용하는 편이 간편하지만, 언제나 프로그래밍에서는 정규화된 상한/하한을 구하는 문제보다는 주어진 문제와 엮어져서 응용하는 문제가 나오기 때문에 아래와 같이 코딩으로 구현해 보는 것이 사고를 확장시킬 수 있는 지름길이 된다.  lower_bound와 upper_bound의 차이점은 if 문의 조건에 '='을 포함하느냐 포함하지 않느냐 밖에 없다. 또한 제일 오른쪽 경계의 값인 r이 n-1이 아닌 n이라는 점도 주목해야 한다. upper_bound와 lower_bound의 개념 자체가 위치를 찾아가기 때문에 현재의 배열의 크기보다 위치는 더 커질 수 있다는 점을 꼭 기억해야 한다. 

int lower_bound(int left, int num) {
    int l = left;
    int r = n;
    while (l<r) {
        int mid = (l+r)/2;
        if (arr[mid] < num) l = mid+1;
        else r = mid;
    }
    return l;
}

int upper_bound(int left, int num) {
    int l = left;
    int r = n;
    while (l<r) {
        int mid = (l+r)/2;
        if (arr[mid] <= num) l = mid+1;
        else r = mid;
    }
    return l;
}

 

[Two-pointer]

 Two-pointer의 방법은 생각보다 복잡한 측면이 있다. 일단 전체적인 흐름은 한개의 수를 먼저 정해 두고 그 수보다 큰 두개의 수를 정하는 방법으로 생각하면 된다. 여기에서 가지치기가 가능한데, 정렬한 상태이기 때문에 처음 선택한 수가 0보다 크면 세 수의 합이 0이 될 방법이 없으므로 과감히 가지치기 한다. Two-pointer는 한 수를 정하고 그보다 큰 수의 처음에서 마지막까지 탐색하는 형태인데, 두 수가 같아질 때까지 while문을 돌리면서 진행하되 합이 0보다 크면 큰수(r)을 감소 시키고, 0보다 작으면 작은수(l)를 증가시키는 식이다. 복잡한건 합이 0일 때이다. 만약 큰수(r)과 작은 수(l)이 같다면 그 중간의 수는 모두 같기 때문에 $_{r-l+1}C_2$ 를 구해서 정답에 포함시켜줘야 하고 그렇지 않은 경우는 큰수(r) 쪽에서 같은 수와 작은(l) 쪽에서 같은 수를 모두 구해서 곱을 통해 모든 경우의 수를 포함해 줘야 한다. 

 위의 예시를 보면 이해가 편하다. 인덱스 i, j, k에서의 값을 더해서 0이 되는 수는 맨 위처럼 index j에서 같은 수가 3개 이고 index k에서 같은 수가 2개라면 모든 경우의 수를 표현해 보면 index j에서 같은 수의 갯수 * index k에서 같은 수의 갯수라는 것을 생각해 볼 수 있다. 

def solve():
    # two pointer method
    sol = 0
    for i in range(n-2):
        if arr[i]>0 : break
        l, r = i+1, n-1
        # print("i: ", i)
        while (l<r):
            _sum = arr[i]+arr[l]+arr[r]
            if _sum > 0:
                r -= 1
            elif _sum < 0:
                l += 1
            else: # 합이 0일 경우
                if arr[r] == arr[l]: # 정렬된 상태에서 두수가 같으면 사이값은 모두 같은 상태
                    sol += (r-l+1)*(r-l)//2 # (r-l+1)C2
                    break
                else: # 그렇지 않으면 l, r에서 하나씩 내려가면서 같은수의 갯수를 탐색
                    r_move, l_move = 0, 0
                    r_value = arr[r]
                    l_value = arr[l]
                    while arr[r] == r_value: # 한번은 무조건 카운팅 되야 한다.
                        r_move += 1
                        r -= 1
                    while arr[l] == l_value: # 마찬가지로 한번은 무조건 카운팅
                        l_move += 1
                        l += 1
                    sol += l_move*r_move # 조합의 갯수를 더해준다.
    return sol

파이썬에서 풀이했음에도 불구하고 $O(n^2)$ 복잡도를 갖는 Two-pointer가 C++에서 $O(n^2log(n))$ 복잡도의 lower_bound && upper_bound보다 속도가 훨씬 빠르다는 것을 확인해 볼 수 있다. 전체 코드는 아래를 참고하자.

<C++> https://github.com/Koo82/Algotirhm/blob/main/%5BBS%5DBJ_3151.cpp

GitHub - Koo82/Algotirhm

<Python> https://github.com/Koo82/Algotirhm/blob/main/%5BBS%5DBJ_3151.py

GitHub - Koo82/Algotirhm